2P_line.py

Description

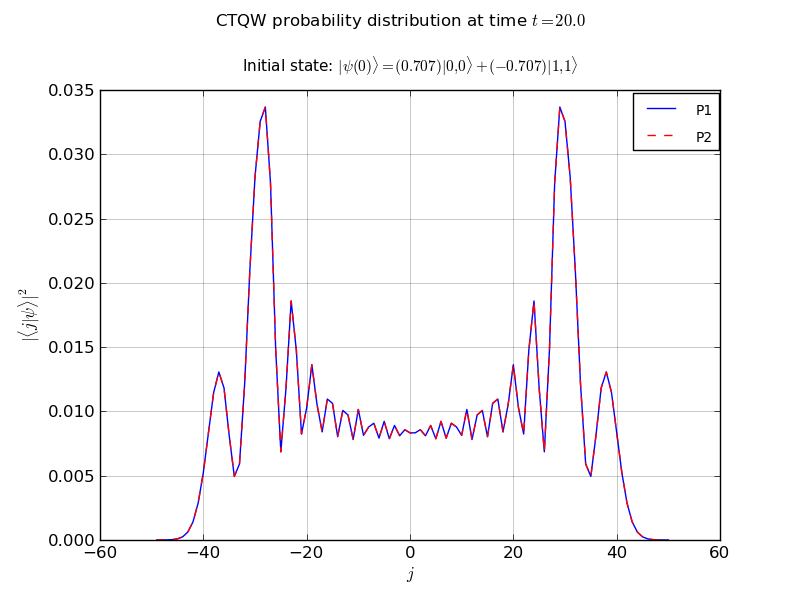
This example propagates a 2 particle continuous-time quantum walk on an infinite line

Amongst the features used, it illustrates:

  • recieving command line options using PETSc

  • the use of the chebyshev algorithm
    • setting the EigSolver tolerance, as well as the minimum eigenvalue

  • adding a diagonal defects to various nodes

  • same-node interactions between particles

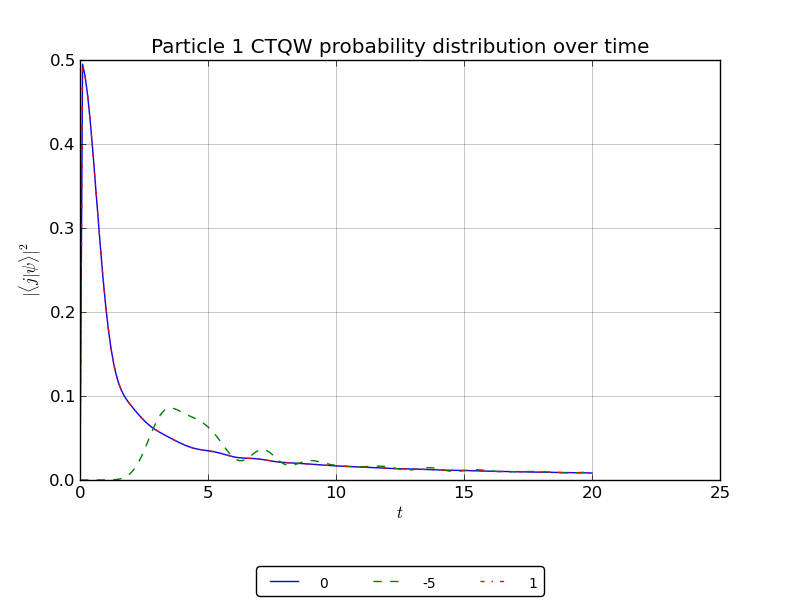
  • creating node handles to watch the probability at specified nodes

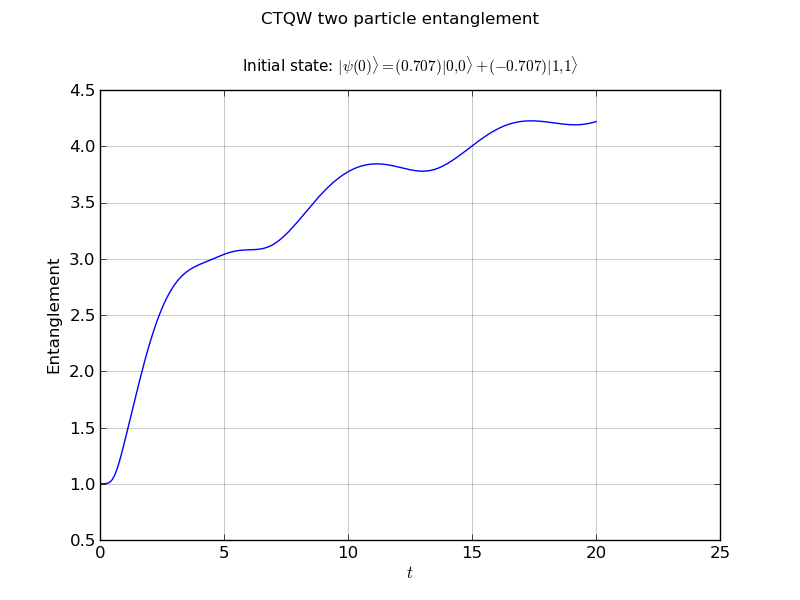
  • creating entanglement handles to watch the entanglement

  • various plotting abilities:
    • probability vs node plots
    • probability vs time plots
    • entanglement vs time plot

  • Exporting the final state to a PETSc binary vector file

Output

../../_images/2p_line_plot.png ../../_images/2p_line_nodes.png ../../_images/2p_line_ent.png

Source Code

[Download source code]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#!/usr/bin/env python2.7
# initialize PETSc
import sys, petsc4py
petsc4py.init(sys.argv)
from petsc4py import PETSc
import numpy as np

# import pyCTQW as qw
import pyCTQW.MPI as qw

# enable command line arguments -t and -N
OptDB = PETSc.Options()
N = OptDB.getInt('N', 100)
t = OptDB.getReal('t', 20)

# get the MPI rank
rank =  PETSc.Comm.Get_rank(PETSc.COMM_WORLD)

if rank == 0:
	print '2P Line\n'

# initialise an N (default 100) node graph CTQW
walk = qw.Line2P(N)

# Create a Hamiltonian with 2P interaction.
walk.createH(interaction=1.)

# create the initial state (1/sqrt(2)) (|0,0>-|1,1>)
init_state = [[0,0,1.0/np.sqrt(2.0)], [1,1,-1.0/np.sqrt(2.0)]]
walk.createInitState(init_state)

# set the eigensolver properties.
walk.EigSolver.setEigSolver(tol=1.e-2)
# underestimate the minimum eigenvalue
walk.EigSolver.setEigSolver(emin_estimate=0)

# create a handle to watch the probability at nodes -5,0,1:
walk.watch([0,1,-5])
# create a handler to watch the entanglement
walk.watch(None,watchtype='entanglement',verbose=False)

# Propagate the CTQW using the Chebyshev method
# for t=100s in timesteps of dt=0.1
for i in np.arange(0.1,t+0.1,0.1):
	walk.propagate(i,method='chebyshev')

# plot the marginal probabilities
# after propagation over all nodes
walk.plot('out/2p_line_plot.png')

# plot the probability over time for the watched nodes
walk.plotNodes('out/2p_line_nodes.png')

# plot the entanglement over time
walk.plotEntanglement('out/2p_line_ent.png')

# export the final state
walk.exportState('out/2p_line_state.bin','bin')

# destroy the quantum walk
walk.destroy()