3P_3cayley.py

Description

../../_images/3cayley2.png

This example propagates a 3 particle continuous-time quantum walk on a 3-cayley tree.

Amongst the features used, it illustrates:

  • recieving command line options using PETSc

  • the use of the chebyshev algorithm, with minimum eigenvalue pre-set

  • adding a diagonal defect to various nodes

  • same-node interactions between particles

  • creating node handles to watch the probability at specified nodes

  • creating entanglement handles to watch the entanglement

  • various plotting abilities:
    • probability vs node plots
    • probability vs time plots
    • graph plots
    • entanglement plots

Output

../../_images/3p_3cayley_plot.png ../../_images/3p_3cayley_nodes_particle1.png ../../_images/3p_3cayley_nodes_particle3.png ../../_images/3p_3cayley_node1.png

Required Files

Source Code

[Download source code]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#!/usr/bin/env python2.7
# initialize PETSc
import sys, petsc4py
petsc4py.init(sys.argv)
from petsc4py import PETSc
import numpy as np

# import pyCTQW as qw
import pyCTQW.MPI as qw

# enable command line arguments -t and -N
OptDB = PETSc.Options()
N = OptDB.getInt('N', 10)
t = OptDB.getReal('t', 5)

# get the MPI rank
rank =  PETSc.Comm.Get_rank(PETSc.COMM_WORLD)

if rank == 0:
	print '3P 3-cayley Tree CTQW\n'

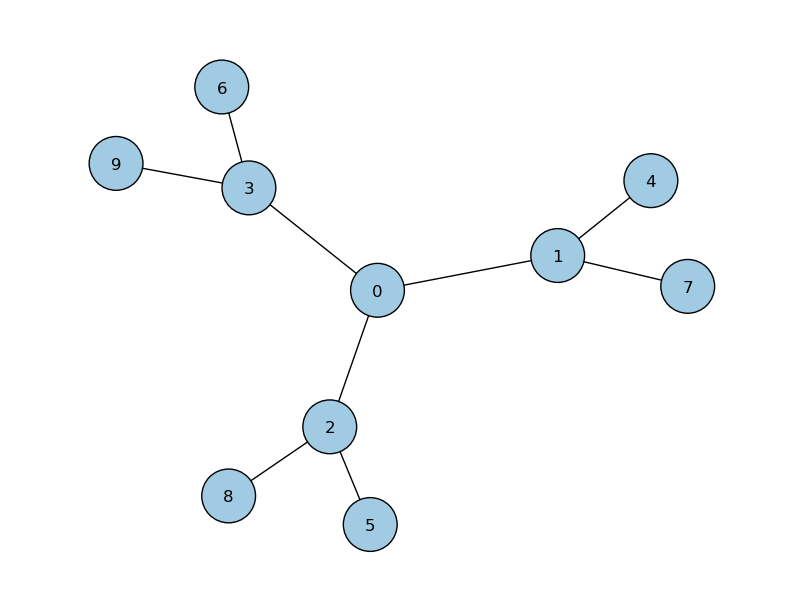
# initialise a 10 node graph CTQW
walk = qw.Graph3P(N)

# Create a 3 particle interacting Hamiltonian from a file.
# A defect of amplitude 2 and 0.5 has
# been added to nodes 3 and 4 respectively.
d = [3,4]
amp = [2.0,1.5]
walk.createH('../graphs/cayley/3-cayley.txt','txt',d=d,amp=amp,layout='spring',interaction=1.5)

# create the initial state (1/sqrt(2)) (|0,1,4>+i|1,1,4>)
init_state = [[0,1,4,1.0/np.sqrt(2.0)], [1,1,4,1.j/np.sqrt(2.0)]]
walk.createInitState(init_state)

# set the eigensolver properties.
#Note that Emin has been set exactly.
walk.EigSolver.setEigSolver(tol=1.e-2,verbose=False,emin_estimate=0.)

# create a handle to watch the probability at nodes 0-4,9:
walk.watch([0,1,2,3,4,9])

# Propagate the CTQW using the Chebyshev method
# for t=5s in timesteps of dt=0.01
for dt in np.arange(0.01,t+0.01,0.01):
	walk.propagate(dt,method='chebyshev')

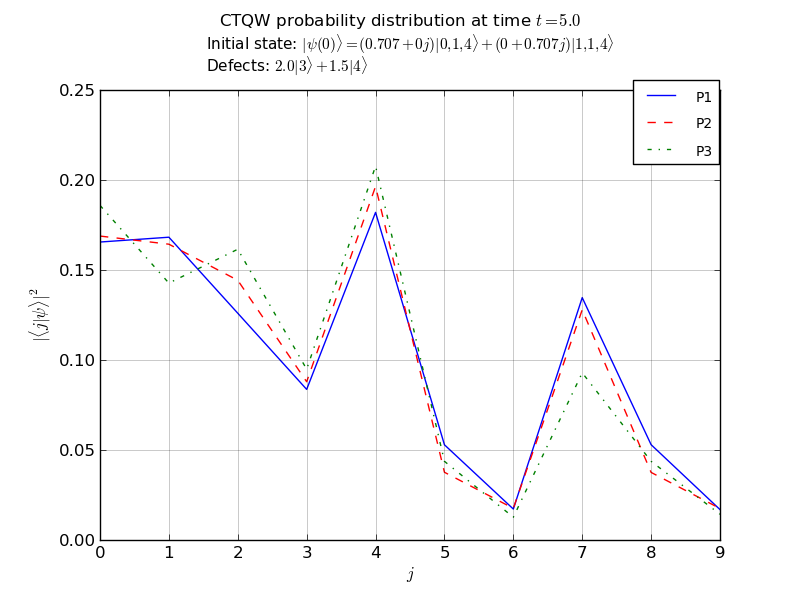
# plot the p1, p2, p3 marginal probabilities
# after propagation over all nodes
walk.plot('out/3p_3cayley_plot.png')

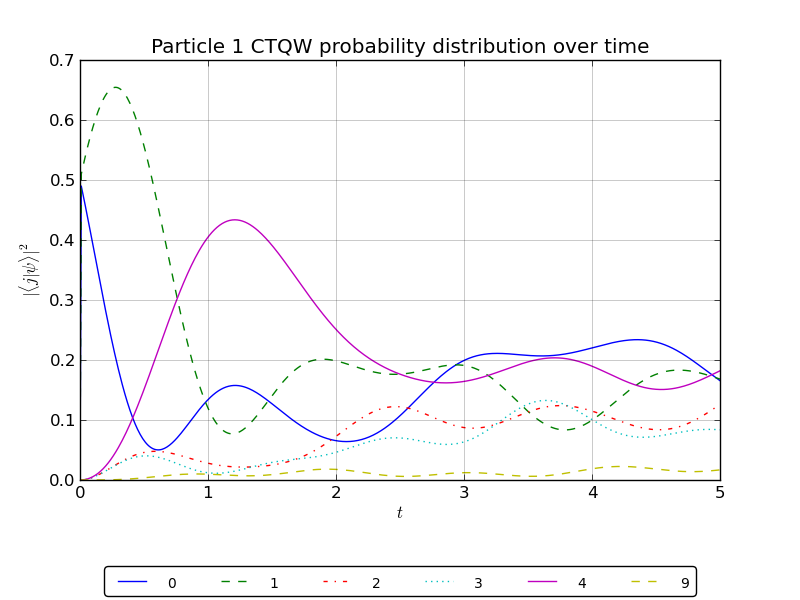
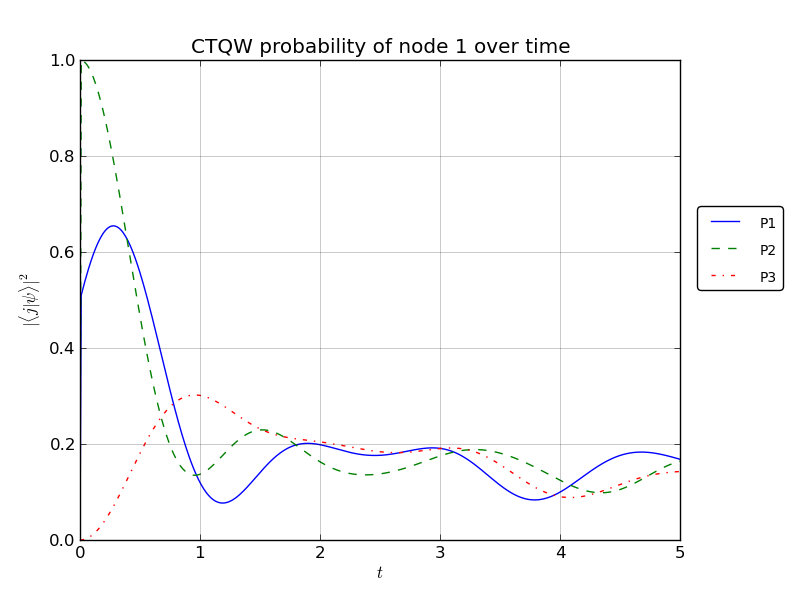
# plot the p1, p2, p3 probability over time for watched node1
walk.plotNode('out/3p_3cayley_node1.png',1)
# plot the particle 1 probability over all watched nodes
walk.plotNodes('out/3p_3cayley_nodes_particle1.png',p=1)
# plot the particle 2 probability over all watched nodes
walk.plotNodes('out/2p_3cayley_nodes_particle2.png',p=2)
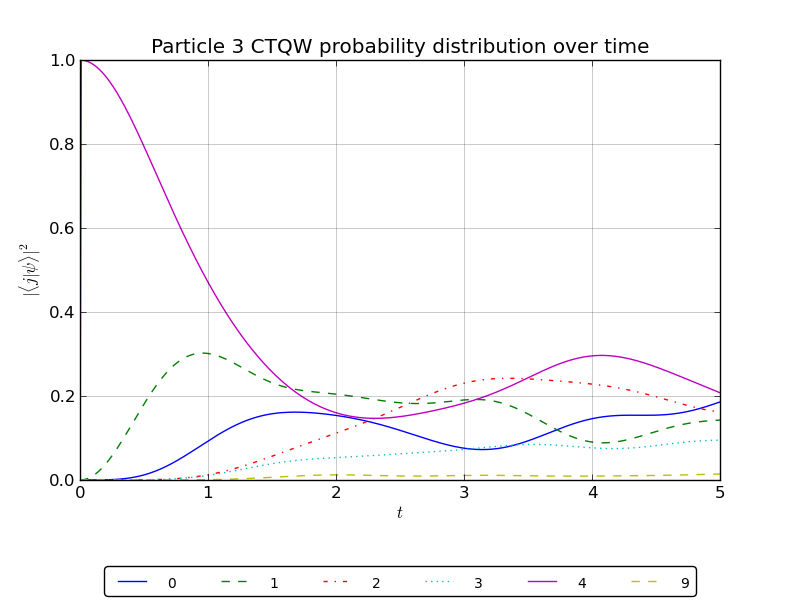
# plot the particle 3 probability over all watched nodes
walk.plotNodes('out/3p_3cayley_nodes_particle3.png',p=3)

# destroy the quantum walk
walk.destroy()