2P_sr.py

Description

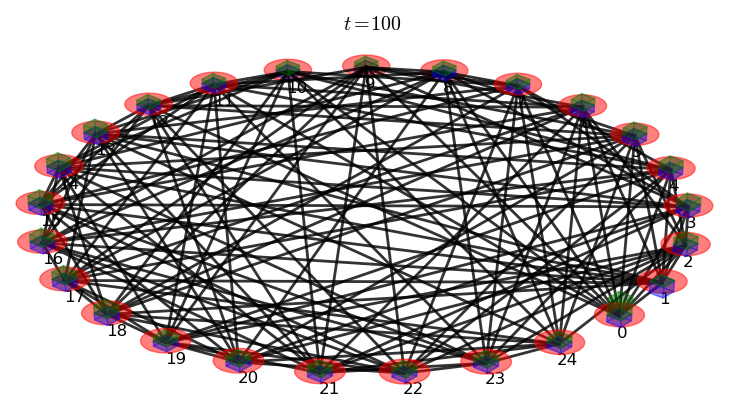
This example propagates a 2 particle continuous-time quantum walk on the first member of the strongly regular \((25,12,5,6)\) family of graphs.

Amongst the features used, it illustrates:

  • the use of the Krylov propagation algorithm

  • various plotting abilities:
    • probability vs node plot
    • probability and graph plot

Output

../../_images/2p_sr_graph.png ../../_images/2p_sr_plot.png

Required Files

Source Code

[Download source code]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#!/usr/bin/env python2.7
# initialize PETSc
import sys, petsc4py
petsc4py.init(sys.argv)
from petsc4py import PETSc
import numpy as np

# import pyCTQW as qw
import pyCTQW.MPI as qw

# get the MPI rank
rank =  PETSc.Comm.Get_rank(PETSc.COMM_WORLD)

if rank == 0:
	print '2P Strong Regular CTQW'

# initialise a 25 node 2P graph CTQW, 
# and create a Hamiltonian from a file.
walk = qw.Graph2P(25)
walk.createH('../graphs/strong-regular-25-12-5-6/1.txt','txt',layout='circle')

# create the initial state (1/sqrt(2)) (|0,1>+i|1,1>)
init_state = [[0,1,1.0/np.sqrt(2.0)], [1,1,1.0j/np.sqrt(2.0)]]
walk.createInitState(init_state)

# Propagate the CTQW using Krylov subspace methods
walk.propagate(100,method='krylov')

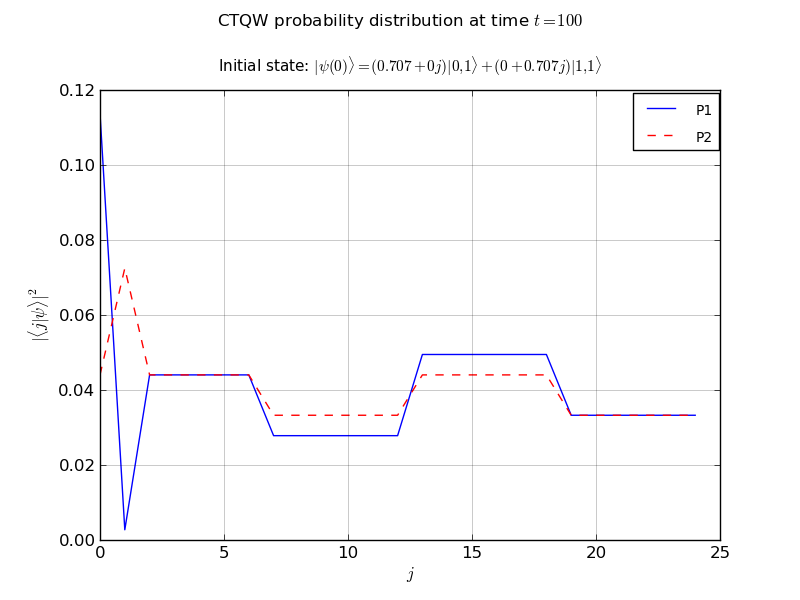
# plot the p1 and p2 marginal probabilities
# after propagation over all nodes
walk.plot('out/2p_sr_plot.png')

# plot a 3D graph representation with bars
# representing p1 and p2 marginal probabilities
walk.plotGraph(output='out/2p_sr_graph.png')

# destroy the quantum walk
walk.destroy()